IndexFiguresTables |
Youngseo Kim , Minseo Yu , Younghan Lee and Ho BaeLabel Differential Privacy Study for Privacy Protection in Multimodal Contrastive Learning ModelAbstract: Recent advancements in multimodal deep learning have garnered significant attention from both academia and industry due to their exceptional accuracy and ability to learn rich knowledge representations. In particular, contrastive learning based approaches have played a pivotal role in dramatically enhancing the performance of multimodal deep learning. However, the use of multiple data sources in multimodal deep learning increases the risk of inferring sensitive information through data fusion, posing a higher privacy invasion attack compared to unimodal deep learning. This challenge cannot be fully addressed by privacy preserving techniques traditionally employed in unimodal deep learning, underscoring the growing importance of privacy protection in this domain. To address this issue, previous studies have relied on trusted execution environments or strengthened security by selectively recording data classified as privacy threatening. However, these approaches face limitations such as hardware dependency, performance degradation, and accuracy issues in data classification. These shortcomings hinder scalability and usability while leaving systems vulnerable to emerging threats. In this study, we address the privacy concerns by applying the Double Randomized Response algorithm, which ensures label differential privacy during the data preparation process. As a result, we achieved 80.14% accuracy in image-table matching and classification tasks, demonstrating a balance between privacy protection and performance. This method is the first to incorporate data security considerations into multimodal deep learning models while substantiating its efficacy, marking a significant contribution to the field. Keywords: Differential Privacy , Multimodal Deep Learning , Contrastive Learning , Data Privacy 김영서†, 유민서†, 이영한††, 배호†††멀티모달 대조 학습 모델의 프라이버시 보호를 위한 라벨 차등 프라이버시 연구요 약: 최근 멀티모달 딥러닝은 뛰어난 정확도와 풍부한 지식 학습 능력으로 학계와 산업계에서 많은 관심을 받고 있다. 특히, 대조 학습 기반 연구들은 멀티모달 딥러닝의 성능을 비약적으로 향상시키며 핵심적인 역할을 하고 있다. 하지만, 다중 데이터 소스를 활용하는 멀티모달 딥러닝은 데이터 간의 결합을 통해 민감한 정보를 추론할 가능성이 커지면서, 단일 모달 딥러닝보다 더 높은 프라이버시 침해 위험을 동반한다. 이는 기존의 단일 모달 딥러닝에서 사용되던 프라이버시 보호 기법만으로는 완전히 해결하기 어려운 문제로, 그 중요성이 날로 커지고 있다. 이 문제를 해결하기 위해 기존 연구에서는 신뢰 실행 환경에 의존하거나, 프라이버시 위협 데이터를 분류 및 선택적으로 기록하여 보안을 강화하지만, 하드웨어의 의존성, 성능 저하, 데이터 분류 정확도 한계 등 문제가 존재한다. 이러한 한계는 확장성과 사용성을 저해하고 새로운 공격에 취약할 가능성이 있다. 본 연구는 프라이버시 문제를 해결하기 위해 데이터 준비 과정에서 라벨 차등 프라이버시를 보장하는 Double Randomized Response 알고리즘 을 적용하였다. 그 결과, 이미지-테이블 매칭 및 분류 작업에서 80.14%의 정확도를 달성하며 프라이버시 보호와 성능 간 균형을 실증하였다. 이 방법은 최초로 멀티모달 딥러닝 모델에 데이터 보안을 고려하였으며 이에 대한 성능을 입증한 의의를 가진다. 키워드: 차등 프라이버시, 멀티모달 딥러닝, 대조 학습, 데이터 프라이버시 1. 서 론초기 인공지능 시스템은 단일 모달리티, 즉 이미지, 텍스트, 음성과 같은 단일 데이터 유형을 입력으로 받아 처리하는 데 초점을 맞췄다. 예를 들어, Convolutional Neural Networks(CNN)는 이미지 데이터를 분석하여 분류 작업을 수행하는 데 효과적이었으며, Recurrent Neural Networks(RNN)는 텍스트 데이터를 기반으로 텍스트 생성, 번역과 같은 자연어 처리 작업에서 두각을 나타냈다. 음성 인식 분야에서는 HMM(Hidden Markov Models), GMM(Gaussian Mixture Models)과 같은 모델이 사용되어 음성을 분석하고 인식하는 데 기여하였다[1]. 그러나 이러한 단일 모달리티 중심의 접근법은 데이터 유형 간의 상호작용을 다루지 못한다는 한계를 가졌다. 이미지, 텍스트, 음성과 같은 다양한 모달리티 데이터 간의 복잡한 관계를 학습할 수 없었기 때문에, 보다 복합적이고 다차원적인 문제를 해결하는 데 제약이 있었다. 현대의 데이터 환경이 요구하는 다중 모달리티 간의 융합과 통합적 분석은 이러한 단일 모달 접근 방식으로는 충분히 대응하기 어려운 과제였다. 이러한 한계를 극복하기 위해 다양한 학습 방식이 발전해왔다. 지도 학습(Supervised Learning)은 라벨링된 데이터를 기반으로 명확한 데이터-라벨 관계를 학습하여 분류와 회귀 같은 작업에서 높은 성능을 보여준다. 하지만 라벨이 없는 데이터에서는 적용이 어려워 한계가 있다. 이를 보완하기 위해 등장한 비지도 학습(Unsupervised Learning)은 라벨 없이도 데이터의 패턴과 구조를 학습할 수 있는 방식이다. 이는 라벨링 비용이 필요 없다는 점에서 효율적이지만, 효과적인 학습을 위해 데이터에 대한 깊은 이해가 요구되며, 다양한 작업에 활용 가능한 표현 학습 능력을 필요로 한다. 자기 지도 학습(Self-Supervised Learning)은 이들 방식의 한계를 극복하기 위해 라벨이 없는 데이터를 스스로 라벨링하여 학습하는 방법이다. 이 방식은 대규모 데이터에서도 효과적인 학습이 가능하다는 점에서 큰 주목을 받았으나, 여전히 단일 모달리티에 초점이 맞춰져 있어 단일 모달리티의 한계를 벗어나지 못했다. 최근 이러한 제약을 해결하고자 멀티모달 딥러닝이 주목받고 있다. 멀티모달 딥러닝은 이미지, 텍스트, 오디오, 테이블 데이터 등 다양한 모달리티 데이터를 통합적으로 학습하여 복잡한 문제를 해결할 수 있는 방법론이다[2]. 예를 들어, 교통사고 발생 가능성을 예측하는 모델을 개발할 때, 단일 모달리티로 차량 센서 데이터를 학습하는 것보다 운전자의 연령, 운전 경력, 도로 상태, 날씨 정보와 같은 다양한 데이터를 함께 활용하면 모델은 더 포괄적이고 정확한 예측을 수행할 수 있다. 또한 뇌졸중과 같은 특정 질병을 진단하는 모델에서는, 단일 모달리티로 뇌 이미지만 학습하는 것보다 환자의 나이, 키, 몸무게, 뇌 검사 데이터 등의 테이블 데이터를 함께 활용하면 모델은 더 풍부한 정보를 학습할 수 있으며, 이로 인해 정확도가 크게 향상될 수 있다[3]. 멀티모달 딥러닝의 장점을 극대화하기 위해 많은 연구가 진행되었으며, 특히 대조 학습(Contrastive Learning)을 기반으로 한 다양한 연구[4-6]가 뛰어난 성과를 기록했다. 하지만, 멀티모달 딥러닝은 단일 모달리티에서는 드러나지 않았던 개인정보가 여러 모달리티의 결합으로 인해 의도치 않게 유출될 위험을 내포하고 있다[7]. 예를 들어, 온라인 쇼핑 플랫폼에서 구매 이력, 검색 기록, 결제 정보 등을 동시에 수집하는 시스템의 경우, 이러한 데이터를 결합하여 사용자의 소비 습관, 경제 상태, 심지어 개인적인 취향과 같은 민감한 정보를 추론할 가능성이 존재한다. 따라서 멀티모달 딥러닝에서는 성능 향상뿐만 아니라 데이터 보안 문제를 동시에 해결해야 한다. 멀티 모달 딥러닝에 보안을 적용한 기존 연구는 신뢰 실행 환경을 활용하여 민감한 데이터를 안전하게 처리하며[8], 프라이버시 위협이 있는 데이터와 그렇지 않은 데이터를 구분하고, 선택적으로 기록하는 알고리즘을 통해 프라이버시를 보호하는 접근 방식이 있다[9]. 그러나 이러한 방법은 특정 하드웨어나 알고리즘에 의존하는 방식이기 때문에 다양한 환경에서 적용이 어려운 한계를 극복하기 위해, 확장성과 사용성이 높은 연구가 필요하다. 한편 기존의 데이터 보안 문제를 해결하기 위해 단일 모달 딥러닝에서 차등 프라이버시(Differential Privacy, DP)[10]를 활용한 연구가 많이 이루어져 왔다[11]. 차등 프라이버시는 통계적 기법을 활용하여 적절한 노이즈를 추가함으로써 결과의 유용성을 유지하면서도 개인 정보를 보호하는 방법이다. 예를 들어, 데이터 집합 A={Alice, Bob, Charlie}와 B={Alice, Bob, David}가 있고, Charlie만이 특정 병원에서 의료 서비스를 받았다고 가정하자. 이때, 데이터 집합 A와 B에 “해당 병원을 이용한 사람의 수”라는 쿼리를 보낸다면 각각 A=1, B=0이라는 답변을 받을 수 있다. 이러한 결과는 Charlie가 해당 병원을 이용했다는 민감한 정보를 드러낼 수 있다. 차등 프라이버시는 이러한 위험을 방지하기 위해 A와 B의 결과에 적절한 노이즈를 추가함으로써 데이터를 구별할 수 없도록 처리하고, 민감한 정보를 보호한다. 이 기법은 입력 데이터에 대한 결과값을 통해 원 데이터를 복원하려는 추론 공격이나 특정 데이터가 학습에 사용되었는지 확인하려는 공격을 방어할 수 있는 강력한 방법론으로 널리 연구되고 있다[12, 13]. 그러나 단일 모달 딥러닝에서 성공적으로 적용된 차등 프라이버시를 멀티 모달 딥러닝에 그대로 적용하는 경우, 서로 다른 모달리티 간의 상관성을 무시하기 때문에 프라이버시 보호의 효과가 제한적일 수 있다[14]. 본 논문에서는 차등 프라이버시의 완화된 형태인 라벨 프라이버시를 활용하여 멀티모달 딥러닝 모델에서 생기는 프라이버시 문제에 대해 해결하고자 한다. 우리는 멀티모달 딥러닝 모델 중 이미지와 테이블 데이터를 사용하는 멀티모달 대조 학습 모델에 라벨 프라이버시를 적용한 새로운 모델을 제안한다. 본 연구는 멀티모달 딥러닝에 라벨 차등 프라이버시를 적용한 최초의 사례로, 성능과 프라이버시 보호 간의 균형을 제시하며 중요한 학문적 기여를 한다. 2. 배 경2.1 대조 학습대조 학습(Contrastive Learning)은 자기 지도 학습의 일종으로, 데이터 간의 유사성을 학습하며 데이터 표현(embedding)을 구축하는 방법이다. 이 방식에서는 유사한 데이터로 이루어진 양성 쌍(positive pair)은 임베딩 간 거리를 최소화하고, 서로 다른 데이터로 구성된 음성 쌍(negative pair)은 임베딩 간 거리를 최대화하는 방향으로 학습이 이루어진다. 이렇게 학습된 표현은 분류와 같은 다양한 후속 작업(downstream task)에 효과적으로 활용될 수 있다. 최근 대조 학습의 응용 가능성과 성능이 크게 발전하면서 다양한 접근 방식이 제안되고 있다. 예컨대, [15]는 라벨 없이 이미지의 유의미한 표현을 학습하는 기법을 소개했으며, 클러스터 할당을 통해 시각적 특징 학습의 효과를 입증했다. 또한, [16]은 비전 트랜스포머에 자기 지도 학습을 접목시켜 기존 학습 모델과 비슷한 수준의 성능을 달성하는 데 성공했다. 한편, [17]에서는 비디오의 여러 모달리티를 사용한 대조 학습을 활용해 강력한 비디오 표현 학습 방식을 제안하며, 멀티모달 대조 학습의 새로운 가능성을 열었다. CLIP[4]은 이미지와 텍스트 간 관계를 학습하는 대표적인 대조 학습 모델이다. 이 모델에서는 이미지 인코더와 텍스트 인코더로 생성된 임베딩 [TeX:] $$z_i \text { 와 } z_t$$를 양성 쌍으로 설정하고, [TeX:] $$z_i$$와 [TeX:] $$z_t^*, z_i^* \text { 와 } z_t$$와 같이 서로 다른 이미지와 텍스트 조합을 음성 쌍으로 구성한다. 이러한 구조를 통해 두 모달리티 간의 관계를 효과적으로 학습할 수 있다. SimCLR[5]에서는 인코더의 출력값을 입력으로 받아 두 개의 Fully Connected layer와 ReLU를 포함하는 projection head를 통해 손실 함수를 정의한다. 이 과정에서 양성 쌍에 대해 projection head의 출력값 [TeX:] $$h_i, h_j$$가 주어질 때 손실 함수는 Equation (1)로 정의되며 [TeX:] $$\operatorname{sim}(u, v)=u^{\mathrm{T}} v /\|u\|\|v\|$$이다.
(1)[TeX:] $$l_{i, j}=-\log \frac{\exp \left(\operatorname{sim}\left(h_i, h_j\right) / \tau\right)}{\sum_{k=1}^{2 N} 1_{[k \neq i]} \exp \left(\operatorname{sim}\left(h_i, h_k\right) / \tau\right)}$$[6]에서 제안된 멀티모달 딥러닝 방법은 CLIP의 접근 방식을 확장하여 한 쌍의 이미지, 테이블 데이터를 양성 쌍으로 설정하고, 나머지 조합을 음성 쌍으로 정의한다. 이 모델은 SimCLR와 동일한 손실 함수를 사용하여 두 모달리티 간의 관계를 효과적으로 학습하도록 설계되었다. 이를 통해 이미지와 테이블 데이터 간의 상호 연관성을 효율적으로 학습한다. 2.2 라벨 차등 프라이버시차등 프라이버시(Differential Privacy)는 데이터 집합에 노이즈를 추가하여 개별 클라이언트의 정보를 보호하면서도 유의미한 통계적 정보 쿼리를 공유할 수 있도록 설계된 기법이다. 여기서 [TeX:] $$\epsilon, \delta$$가 0보다 큰 값이고 [TeX:] $$D_1 \text { 과 } D_2$$가 하나의 구성 요소만 다른 데이터 집합이라고 가정하자. 메커니즘 M을 적용했을 때의 결과가 [TeX:] $$O \in \operatorname{Range}(M)$$일 경우, 아래의 Equation(2)이 성립한다면 “메커니즘 M이 ([TeX:] $$\epsilon, \delta$$)-differential privacy (DP)를 만족한다”라고 정의된다.
(2)[TeX:] $$\operatorname{Pr}\left[M\left(D_1\right) \in O\right] \leq e^\epsilon \times \operatorname{Pr}\left[M\left(D_2\right) \in O\right]+\delta .$$일반적으로 차등 프라이버시는 머신러닝과 딥러닝에서 데이터 전체를 보호하는 데 사용되지만, 특정 상황에서는 이러한 접근이 과도하거나 비효율적일 수 있다. 이를 해결하기 위해, 우리는 차등 프라이버시의 완화된 형태인 라벨 차등 프라이버시를 활용하고자 한다. 라벨 차등 프라이버시(Label Differential Privacy)에서의 라벨은 주로 민감한 정보로 간주되어 보호하지만 입력 데이터 포인트의 속성(feature)은 민감하지 않은 공개된 정보이다. [TeX:] $$\epsilon, \delta$$가 0보다 큰 수이고 [TeX:] $$D_{L_1} \text { 과 } D_{L_2}$$가 하나의 구성 요소의 라벨이 다른 데이터 집합이라고 가정하자. 메커니즘 M에 적용했을 때의 결과가 [TeX:] $$O \in \operatorname{Range}(M)$$일 때, 아래의 Equation (3)이 성립한다면 “메커니즘 M이 [TeX:] $$(\epsilon, \delta)$$-label differential privacy (label-DP)를 만족한다”라고 한다.
(3)[TeX:] $$\operatorname{Pr}\left[M\left(D_{L_1}\right) \in O\right] \leq e^\epsilon \times \operatorname{Pr}\left[M\left(D_{L_2}\right) \in O\right]+\delta$$2.3 라벨 Renyi 차등 프라이버시본 논문에서는 [12]에서 소개된 Renyi 차등 프라이버시 (Renyi Differnetial Privacy)를 적용한다. Renyi 차등 프라이 버시에 사용되는 Renyi α-divergence는 모든 α > 1에 대하여 분포 P와 Q 사이의 Renyi α-divergence는 Equation (4)을 만족한다.
(4)[TeX:] $$D_\alpha(P| | Q)=\frac{1}{\alpha-1} \log E_{z \sim Q}\left[\left(\frac{P(z)}{Q(z)}\right)^\alpha\right]$$만약, M이 랜덤 함수인 메커니즘이라고 한다면 [TeX:] $$M\left(z\right) \text { 와 } M\left(z^{\prime}\right)$$ 분포에 대한 Renyi α-divergence는 [TeX:] $$D_\alpha\left(M(z)| | M\left(z^{\prime}\right)\right)$$로 작성된다. Renyi 차등 프라이버시의 정의는 다음과 같다. α > 1이고 [TeX:] $$\epsilon \geq 0$$일 때, 메커니즘 [TeX:] $$M: X \times Y \mapsto X \times Y$$은 모든 [TeX:] $$x, x^{\prime} \in X, y, y^{\prime} \in Y$$에 대해 Equation (5)를 만족하면 “[TeX:] $$(\alpha, \epsilon)$$-Renyi differential privacy(RDP)를 만족한다.”라고 말한다.
(5)[TeX:] $$D_\alpha\left(M(x, y)|\quad| M\left(x^{\prime}, y^{\prime}\right)\right) \leq \epsilon$$이 방법은 기존[10]에서 정의된 차등 프라이버시보다 더 정교하고 유연한 프라이버시 분석이 가능한 확장된 버전이다. α의 값이 더 큰 경우에 강력한 프라이버시를 보장한다. 더불어, [TeX:] $$(\infty, \epsilon)$$-RDP는 [TeX:] $$\epsilon$$-DP와 동등하며, [TeX:] $$(\alpha, \epsilon)$$-RDP는 [TeX:] $$\left(\epsilon^{\prime}, \delta\right)$$-DP에서의 모든 [TeX:] $$\delta \in(0,1) \text { 와 } \epsilon^{\prime}=\epsilon+\frac{\log (1 / \delta)}{\alpha-1}$$임을 알 수 있다[13]. Renyi 차등 프라이버시를 기반으로 한 정적인 특징을 사용한 라벨 차등 프라이버시는 다음 정의를 따른다. α > 1이고 [TeX:] $$\epsilon \geq 0$$일 때, 메커니즘 [TeX:] $$M: X \times Y \mapsto X \times Y$$은 모든 [TeX:] $$x, \in X, y, y^{\prime} \in Y$$에서 아래 Equation (6)을 만족하면 "[TeX:] $$(\alpha, \epsilon)$$-label Renyi differential privacy(label-RDP)를 만족한다.”라고 말한다[13].
(6)[TeX:] $$D_\alpha\left(M(x, y)|\quad| M\left(x^{\prime}, y^{\prime}\right)\right) \leq \epsilon$$반면, 기존[18]에서 사용되는 라벨 차등 프라이버시는 [13]을 통해 라벨 추론 공격에 취약함이 확인되었다. 라벨 추론 공격으로 라벨이 공개되지 않더라도 입력 데이터의 특징이 공개된다면 라벨이 보호되지 않는다. [13]에서는 이를 해결하기 위해 조건부 특징을 고려한 라벨 차등 프라이버시를 다음과 같이 정의한다. α > 1이고 [TeX:] $$\epsilon \geq 0$$이고, P가 X × Y에 대한 분포라고 가정한다. 메커니즘 [TeX:] $$M: X \times Y \mapsto X \times Y$$가 모든 [TeX:] $$y, y^{\prime} \in Y$$에서 Equation (7)를 만족하면 “[TeX:] $$(\alpha, \epsilon, P)$$-label Renyi differential privacy(label-RDP)를 만족한다.”라고 말한다.
(7)[TeX:] $$D_\alpha\left(M\left(f_P(y), y\right)|\quad| M\left(f_P\left(y^{\prime}\right), y^{\prime}\right)\right) \leq \epsilon$$이때, [TeX:] $$f_P: Y \rightarrow X$$는 입력 y를 받아 [TeX:] $$P_{X \mid y}$$에 따라 x를 출력하는 랜덤 합수이다. 이 정의를 사용하면 특징이 공개되지 않은 라벨에 의존하는 분포를 통해 무작위로 추출되기 때문에 라벨 추론 공격을 방지할 수 있다. 3. 방 법본 논문에서는 멀티모달 딥러닝에서의 프라이버시 문제를 해결하기 위해 멀티모달 대조 학습에 라벨 Renyi 차등 프라이버시를 적용해 보고자 한다. 여기서는 이미지 데이터와 테이블 데이터를 활용하는 사례를 가정한다. 두 모달리티 데이터를 페어링하기 전에, 이미지 데이터에 라벨 차등 프라이버시를 적용하여 프라이버시 보호를 보장한다. 기존 연구[13]에서 제시한 double randomized response(double-RR) 알고리즘(Algorithm 1)은 라벨 RDP를 만족하기 위한 핵심 기술로, 이미지 데이터와 라벨에 대해 순차적으로 두 단계의 Randomized Response(RR)를 적용한다. Algorithm 1의 1-5번째 줄에서는 이미지 데이터 [TeX:] $$x \in X$$와 라벨 [TeX:] $$y \in Y$$에 대해 첫 번째 RR을 수행하는데 이 과정에서 y는 1-λ 확률로 원래 값을 유지하며, λ 확률로 다른 무작위 값을 선택한다. 이는 원본 데 이터와 라벨 간의 직접적인 매핑을 교란시켜 프라이버시를 보호하기 위함이다. 두 번째 RR은 Algorithm 1의 6-11번째 줄에서 일어난다. x에 대하여 일반적인 RR를 기본적으로 동일한 방식을 유지하며 단순히 균일한 분포에서 무작위 값을 선택하지 않고 λ의 확률이라면, k-최근접 이웃(k-NN) 알고리즘을 사용하여 자신과 최대한 유사한 샘플을 선택할 확률을 높이도록 하였다. 즉, 자기 자신이 아닌 [TeX:] $$\tilde{x}$$을 뽑을 때, [TeX:] $$P_{X \mid {y^\prime}}$$의 분포에서 k-NN 알고리즘으로 가까운 데이터 중에 하나로 선택하도록 하였다. Algorithm 1은, α > 1이고 P가 X × Y에 대한 분포일 때, Equation (8)이 만족하면 모든 label [TeX:] $$y \in Y$$에 대해 [TeX:] $$(\alpha, \epsilon, P)$$-label RDP를 만족한다. 이는 [13]의 appendix E.에서 증명할 수 있다.
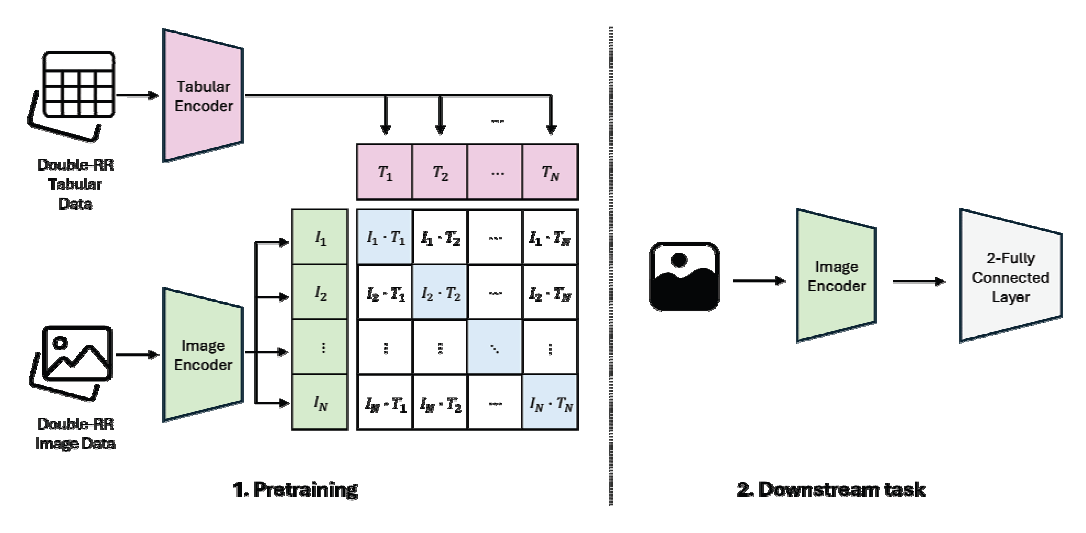
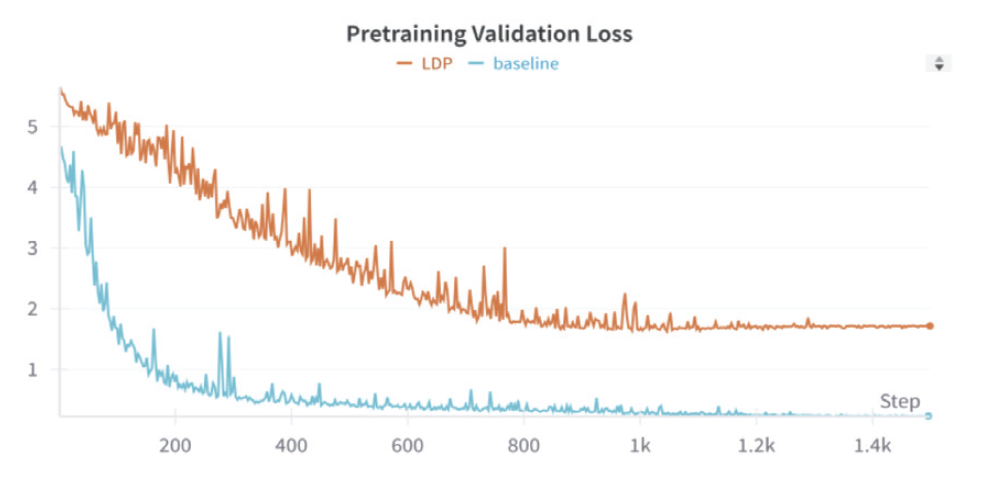
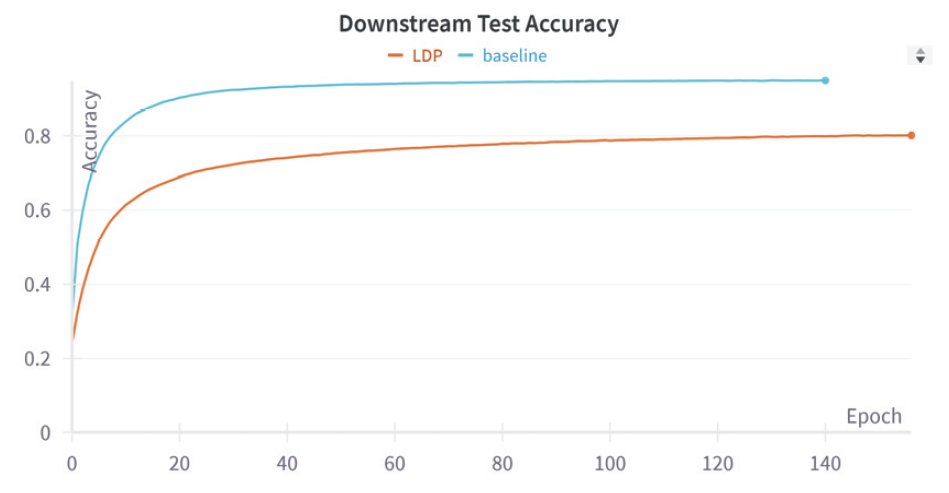
Algorithm 1에서 Double-RR 알고리즘을 활용하여 라벨 차등 프라이버시를 충족하는 이미지 데이터셋을 생성하고, 동일한 인덱스를 가진 테이블 데이터셋을 인코더를 통해 잠재 공간에서 페어링하였다. 이후, CLIP 손실을 사용한 대조 학습을 통해 두 모달리티 간의 연관성을 학습하였다. 이 과정에서 테이블 데이터는 이미지 인코더의 학습을 지원하기 위한 사전 학습 (pretraining) 단계에서만 사용되며, 최종 목표가 이미지 분류이므로 라벨 차등 프라이버시는 이미지 데이터셋에만 적용된다. 학습 프로세스는 Fig. 1과 같이 Algorithm 1을 기반으로 두 단계로 구성된다. 1. 사전 학습(pretraining) 단계에서는 [6]에서 제안된 Self-supervised Contrastive Learning using Random Feature Corruption(SCARF) 방식을 따라 인코더를 학습한다. 테이블 데이터에 적용되는 대조 학습 방법에서, 이미지 도메인에 흔히 사용되는 증강을 위한 변형 방법이 직접 적용되기 어렵다. 변형된 데이터는 원본 샘플과 같은 의미를 유지해야하고, 랜덤하게 선택된 특징을 변형하여 새로운 샘플을 생성한다. 변형된 특징 값은 데이터셋 내에서 해당 열의 값들로부터 샘플링하는 방식을 사용하여 생성된다. 이미지와 테이블 데이터 한 쌍을 양성 쌍으로 정의하며, 나머지 조합은 음성 쌍으로 설정한다. SimCLR 방식을 기반으로 한 손실 함수를 활용하여 모델이 두 모달리티 간의 연관성을 효과적으로 학습하도록 한다. 2. 후속 작업(downstream task)에서는 학습된 인코더를 활용하여 데이터 분류 작업을 수행한다. 이 단계의 목표는 사전 학습에서 학습된 이미지 인코더가 최적의 분류 성능을 보이도록 하는 것이다. 4. 실 험실험에 사용된 데이터셋은 DVM-car 데이터셋[19]으로, 총 1,451,754개의 크기 300x300 자동차 이미지로 구성되어 있다. 본 연구에서는 클래스별 샘플 개수가 최소 50개 이상이며 테이블 데이터에 결측값이 없는 176,414개를 선정하여 데이터를 분할하였다. 선정된 데이터는 절반인 88,207개를 테스트 데이터로 사용하고, 나머지 절반에서 10%인 8,820개를 검증 데이터로, 나머지 79,387개를 학습 데이터로 활용하였다. 테이블 데이터는 각 이미지 데이터와 일대일로 대응되는 데이터로 구성하였다. 실험 환경은 [6]과 동일하게 설정되었다. 데이터 증강은 이미지 데이터와 테이블 데이터에 대해 다음과 같이 수행되었다. 1) 이미지 데이터 증강: 수평 뒤집기, 45도 회전, 각각 0.5의 확률로 무작위로 128x128 크롭을 적용 후 밝기와 대비를 최대 0.5 범위에서 변경하였다. 2) 테이블 데이터 증강: 자동차의 높이, 길이, 너비, 휠베이스와 같은 클래스 식별 열을 최대 50mm 범위에서 무작위로 변형하였으며 다변량 대치법을 사용하여 결측값을 처리하였다. 이런 방식을 통해 이미지와 테이블 데이터의 특성을 보존하면서도 모델 학습에 유용한 데이터 다양성을 확보하였다. 학습 설정에서 학습률은 3.00E-03으로, 가중치 감쇠는 1.50E-06으로 설정하여 모델 학습 안전성과 과적합 방지를 동시에 고려하였다. 배치 크기는 512로 설정하고, 최적화 알고리즘으로는 Adam을 사용하였다. 학습 과정에서 각 step마다 사전 학습을 통해서 잠재 공간을 학습했으며, 그 결과를 바탕으로 epoch 단위에서 후속 작업의 분류 정확도를 측정하였다. Fig. 2는 사전 학습 동안 발생한 변화를 step 단위로 시각화한 그래프이다. 후속 작업의 평가 결과에 해당하는 Fig. 3은 x축은 epoch 단위로 구성하였고 약 12개의 step으로 하나의 epoch가 구성된다. 실험에서는 라벨 차등 프라이버시의 epsilon 값을 5, knn의 k의 값은 3으로 설정했다. 라벨 차등 프라이버시를 적용한 모델과 그렇지 않은 모델 간의 모든 파라미터는 동일하게 유지되었지만, early stopping으로 인해 두 모델의 epoch 수는 각각 500과 444로 달랐다. 정확도 추이에 대한 상세한 결과는 Fig. 2, Fig. 3, Table 1를 통해 확인할 수 있다. [6]에서 제안된 Multi-modal Imaging 모델을 Baseline 모델로 사용하였다. Table 1. Multimodal Contrastive Learning Accuracy
사전 학습은 이미지와 테이블 간의 각각의 인코더와 projection head를 통해 잠재 공간으로 매핑하고, 모달리티 간 임베딩의 코사인 유사도를 극대화하는 CLIP 기반 손실 함수를 사용한다. Table 1에서 사전 학습 결과는 사전 학습을 진행한 모델에 Logistic Regression을 붙여 분류 정확도를 작성하였다. 후속 작업은 사전 학습된 모델의 출력 임베딩을 사용해 2개의 fully connected layer로 구성된 Multi Layer Perceptron을 적용하여 분류 정확도를 측정하였다. Table 1에서의 baseline은 93.00으로 기존 [6]에서 보고된 값과 일치한다. Baseline 모델과 라벨 차등 프라이버시를 적용하지 않은 모델인 Non-LDP는 동일한 실험 환경에서 실험이 진행되었다. 결과에서는 Non-LDP가 1.08 정도로 좀 더 높은 성능을 보였다. 1.08 정도의 차이가 발생한 것은 멀티 GPU의 사용 및 세부 설정의 차이인 것으로 보이며, 이를 통해 실험 세팅이 적절하게 이루어져 있음을 시사한다. 최종적으로, Table 1에서 라벨 프라이버시가 적용된 모델인 LDP와 Non-LDP 간의 정확도는 사전 학습 단계에서는 10.41, 후속 작업 단계에서는 14.84의 성능 손실이 발생한 것을 확인하였다. 일반적으로 차등 프라이버시를 적용하면 프라이버시가 강화는 되지만 정확도가 어느 정도 성능 손실이 불가피하다. 그럼에도 불구하고, 라벨 차등 프라이버시가 적용된 멀티모달 대조 학습 모델이 80% 이상의 정확도를 달성한 것은 매우 긍정적인 결과라고 할 수 있다. 이 결과는 멀티모달 딥러닝에서 성능 저하를 최소화하면서 프라이버시 보호를 유지함을 보이기에 성공적인 모델의 성능과 프라이버시 성공적인 균형을 맞췄기에 큰 의의가 있다. 5. 논 의본 연구에서는 멀티모달 대조 학습에 double randomized response 알고리즘을 적용해 라벨 차등 프라이버시를 충족시켰음을 입증하였다. 이는 기존 연구에서 시도되지 않았던 혁신적인 접근으로, 중요한 기여를 했다. 그러나 본 연구는 테이블 데이터에 대해서는 별도의 차등 프라이버시가 적용되지 않고, 이미지 데이터의 라벨에만 프라이버시 보호를 적용하는데 그쳤다는 한계를 지닌다. 즉, 프라이버시 보호의 범위가 특정 값인 라벨로 국한되어 있어 이미지-오디오-테이블 등의 실질적 다수의 멀티모달을 적용할 때에도 데이터 전체의 포괄적인 보호를 다루지 못한다. 이처럼 라벨 차등 프라이버시를 최초로 도입했다는 점은 학문적, 실질적으로 의미가 크지만, 향후 연구는 이러한 한계를 넘어설 필요가 있다. 특히, 특정 값에 국한되지 않고 전체 데이터셋을 아우르는 일반 차등 프라이버시를 충족시키는 방향으로 확장하는 것이 요구된다. 6. 결 론멀티모달 딥러닝은 다중 데이터 소스를 사용하여 단일모달 딥러닝보다 뛰어난 성능으로 인해 많은 관심을 받고 있다. 하지만 프라이버시를 위해 멀티모달 딥러닝에 기존 단일 모달 딥러닝의 보호 방법을 그대로 적용하기에는 어려움이 있다. 멀티모달 딥러닝의 프라이버시 보호를 위해 신뢰 실행 환경에 의존하거나, 프라이버시 위협 데이터의 분류하여 사용하는 기존의 연구들이 있지만 이는 선택적인 환경에서만 사용 가능한 한계점이 존재한다. 이를 해결하기 위해 라벨 차등 프라이버시를 멀티모달 대조 학습에 double randomized response 알고리즘을 적용해 프라이버시를 보호하였다. 라벨 차등 프라이버시를 적용하지 않았을 때와 적용했을 때의 라벨 분류 정확도가 각각 94.08, 80.14로 14.84의 손실 성능이 발생하였다. 일반적으로 프라이버시 기법을 적용하면 어느 정도 손실은 불가피하기에 프라이버시가 적용된 멀티모달 딥러닝 모델이 80% 이상의 정확도를 보여 매우 우수한 결과로 평가된다. BiographyBiographyBiographyBiography배 호https://orcid.org/0000-0002-5238-3547 e-mail:hobae@ewha.ac.kr 2007년, Computer Science, University College London, UK(학사) 2009년 Information Security, University College London, UK(석사) 2012년∼2016년 SAP Labs 2021년 서울대학교 자연과학대학(박사) 2021년∼현 재 이화여자대학교 사이버보안학과 교수 관심분야: Artificial Intelligence Security, Data Security, Private Synthetic Data, Differential Privacy References
|
StatisticsCite this articleIEEE StyleY. Kim, M. Yu, Y. Lee, H. Bae, "Label Differential Privacy Study for Privacy Protection in Multimodal Contrastive Learning Model," The Transactions of the Korea Information Processing Society, vol. 14, no. 5, pp. 289-296, 2025. DOI: https://doi.org/10.3745/TKIPS.2025.14.5.289.
ACM Style Youngseo Kim, Minseo Yu, Younghan Lee, and Ho Bae. 2025. Label Differential Privacy Study for Privacy Protection in Multimodal Contrastive Learning Model. The Transactions of the Korea Information Processing Society, 14, 5, (2025), 289-296. DOI: https://doi.org/10.3745/TKIPS.2025.14.5.289.
TKIPS Style Youngseo Kim, Minseo Yu, Younghan Lee, Ho Bae, "Label Differential Privacy Study for Privacy Protection in Multimodal Contrastive Learning Model," The Transactions of the Korea Information Processing Society, vol. 14, no. 5, pp. 289-296, 5. 2025. (https://doi.org/https://doi.org/10.3745/TKIPS.2025.14.5.289)
|


 Korean
Korean